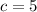Answer:
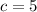
Explanation:
Given
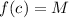
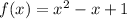
![Interval: [1,8]](https://img.qammunity.org/2022/formulas/mathematics/college/qeij4ytqo6d1lvxzdwthepi1qutoethzdw.png)
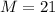
Required
Find c using Intermediate Value theorem
First, check if the value of M is within the given range:
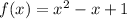
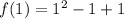
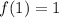

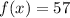
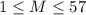

M is within range.
Solving further:
We have:
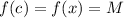
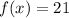
Substitute 21 for f(x) in
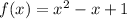
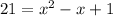
Express as quadratic function
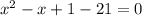
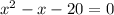
Expand
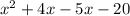
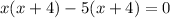
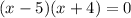
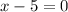 or
or
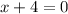
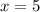 or
or
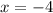
The value of
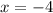 is outside the
is outside the
![Interval: [1,8]](https://img.qammunity.org/2022/formulas/mathematics/college/qeij4ytqo6d1lvxzdwthepi1qutoethzdw.png)
So:
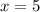
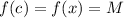
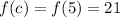
By comparison: