Question

The population of watesville decreases at a rate of 1.6% each year if the population was 62,500 in 2015 what will it be in 2021

Answer 1

Explanation:

We need to first find the model for this particular situation, knowing that this is an exponential decay problem. The main equation for exponential growth/decay (as far as population goes for our problem) is

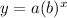`y=a(b)^x` where a is the initial population, b is the rate of decrease in the population which can also be written as (1 - r), y is the population after a certain amount of time, x, goes by. We will let year 2015 = 0 so year 2021 can = 6. This keeps our numbers lower and doesn't change the answer!

Our initial population in the year x = 0 is 62500. Our rate of decay is

(1 - .016) so our b value is .984

Filling in to find our model:

`y=62500(.984)^x`

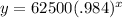
Now we can use that model and sub in a 6 for x to find the population in the year 2021:

`y=62500(.984)^6` and

y = 62500(.9077590568) so

y = 56734.9 or, rounded to the nearest person, 56735