Question

A person is standing close to the edge on a 56 foot building and throws the ball vertically upward. The quadratic function h(t)=-16^2+104t+56 models the balls height above the ground,h(t),in feet, T seconds after it was thrown

what is the maximum height of ball.=
How many seconds did it take to hit the ground=
Please help!

Answer 1

Part 1)

225 feet.

Part 2)

7 seconds.

Explanation:

The height h(t) of the ball above the ground after t seconds is modeled by the function:

`h(t)=-16t^2+104t+56`

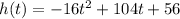
Part 1)

We want to determine the maximum height of the ball.

Notice that the function is a quadratic with a negative leading coefficient, so its maximum will be at its vertex point.

The vertex of a parabola is given by:

`\displaystyle \text{Vertex} = \left(-(b)/(2a), f\left(-(b)/(2a)\right)\right)`

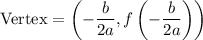
In this case, a = -16, b = 104, and c = 56.

Find the x- (or rather t-) coordinate of the vertex. So:

`\displaystyle t=-((104))/(2(-16))=(104)/(32)=(13)/(4)=3.25\text{ seconds}`

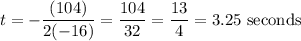
In other words, the ball reaches its maximum height after 3.25 seconds.

To find the maximum height, substitute this value back into the function. Hence:

`\displaystyle h(3.25)=-16(3.25)^2+104(3.25)+56=225\text{ feet}`

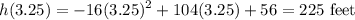
The maximum height of the ball is 225 feet in the air.

Part 2)

We want to find the amount of time it took for the ball to hit the ground.

When the ball hit the ground, its height above the ground is zero. Therefore, we can set h(t) to 0 and solve for t:

`0=-16t^2+104t+56`

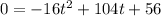
We can simplify a bit. Divide both sides by -8:

`0=2t^2-13t-7`

We can factor. Find two numbers that multiply to 2(-7) = -14 and add to -13.

-14 and 1 works! Therefore, split the second term into -14 and 1:

`\displaystyle 0=2t^2-14t+t-7`

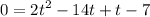
Factor out a 2t from the first two terms and group the last two terms:

`0=2t(t-7)+(t-7)`

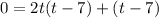
Factor by grouping:

`0=(2t+1)(t-7)`

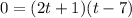
Zero Product Property:

`2t+1=0\text{ or } t-7=0`

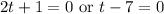
Solve for each case:

`\displaystyle t=-0.5\text{ or } t=7`

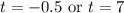
Since time cannot be negative, we can ignore the first case.

Therefore, it takes seven seconds for the ball to hit the ground.