Answer:
35.4 cm
Step-by-step explanation:
We have that when the level of mercury on either limb is the same, the pressure of the trapped air, P₁ = Atmospheric pressure
Also the initial height of the mercury in the tube = The reading of the barometer = 75.0 cm
The initial length of the air column, l₁ = 6.3 cm
The final length of the air column, l₂ = 4.2 cm (The length is expected to decrease due to compression)
The volume, V = l × A
Where;
A = The cross sectional area of the tube
Therefore, the volume of the air column is directly proportional to the length of the air column
∴ V ∝ l
According to Boyles law, we have;
P₁·V₁ = P₂·V₂
Where;
P₁ = The initial pressure in the air column before more mercury is added
V₁ = The initial volume occupied by the air in the air column
P₂, and V₂ are the final pressure and volume of the air column respectively
Given that V = l·A, we can write;
P₁·l₁·A = P₂·l₂·A
P₂ = P₁·l₁·A/(l₂·A) = P₁·l₁/(l₂) = P₁ × 6.3/4.2 = 1.5·P₁
The pressure in the air column after more mercury is added, P₂ = 1.5 × P₁
P₁ = Atmospheric pressure, therefore;
The pressure in the air column after more mercury is added, P₂ = 1.5 × Atmospheric pressure
Pressure = h·ρ·g
Where;
ρ = The density of the substance
g = The acceleration due to gravity
h = The height of the column of the fluid
Given that the density and the gravitational force, can be taken as constant, we have that the pressure of the fluid is directly proportional to the height of the fluid column
Therefore, when the pressure doubles, the height of the fluid column doubles, and when the factor of increase is 1.5, we have;
The final level of the mercury, h₂ = 1.5·h₁ = 1.5×75 cm = 112.5 cm
The initial length of the closed end of the J tube,
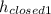 = 6.3 cm + 75 cm = 81.3 cm
= 6.3 cm + 75 cm = 81.3 cm
The final length of the mercury in the closed end,
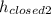 = 81.3 cm - 4.2 cm = 77.1 cm
= 81.3 cm - 4.2 cm = 77.1 cm
The difference in the level of mercury, Δh = h₂ -
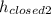
∴ Δh = 112.5 cm - 77.1 cm = 35.4 cm
The difference in the levels of mercury in the limbs, Δh = 35.4 cm