Question

Solve in attachment .​

Answer 1

Explanation:

`thank \: you`

Answer 2

2 ( Option A )

Explanation:

The given integral to us is ,

`\longrightarrow \displaystyle \int_0^1 5x √(x)\ dx`

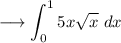
Here 5 is a constant so it can come out . So that,

`\longrightarrow \displaystyle I = 5 \int_0^1 x √(x)\ dx`

Now we can write √x as ,

`\longrightarrow I = \displaystyle 5 \int_0^1 x . x^{(1)/(2)} \ dx`

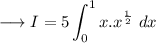
Simplify ,

`\longrightarrow I = 5 \displaystyle \int_0^1 x^{(3)/(2)}\ dx`

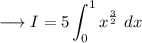
By Power rule , the integral of x^3/2 wrt x is , 2/5x^5/2 . Therefore ,

`\longrightarrow I = 5 \bigg( (2)/(5) x^{(5)/(2)} \bigg] ^1_0 \bigg)`

On simplifying we will get ,

`\longrightarrow \underline{\underline{ I = 2 }}`