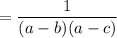Answer:
See Below.
Explanation:
Problem 1)
We want to simplify:
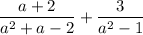
First, let's factor the denominators of each term. For the second term, we can use the difference of two squares. Hence:
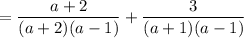
Now, create a common denominator. To do this, we can multiply the first term by (a + 1) and the second term by (a + 2). Hence:
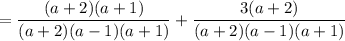
Add the fractions:
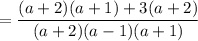
Factor:
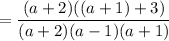
Simplify:
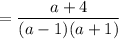
We can expand. Therefore:
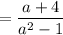
Problem 2)
We want to simplify:
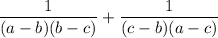
Again, let's create a common denominator. First, let's factor out a negative from the second term:
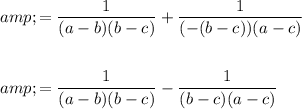
Now to create a common denominator, we can multiply the first term by (a - c) and the second term by (a - b). Hence:
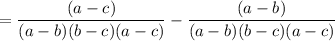
Subtract the fractions:
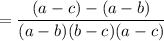
Distribute and simplify:
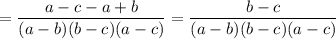
Cancel. Hence: