Answer:
The area of the rectangle is increasing at a rate of 169 cm²/s
Explanation:
Given;
increase in the length of the rectangle,

increase in the width of the rectangle,
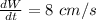
length, L = 15 cm
width, W = 7 cm
The increase in Area is calculated as;
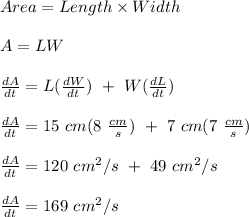
Therefore, the area of the rectangle is increasing at a rate of 169 cm²/s