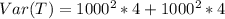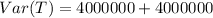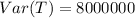The number of hurricanes that will hit a certain house in the next ten years is Poisson distributed with mean 4. Each hurricane results in a loss that is exponentially distributed with mean 1000. Losses - QAmmunity.org

The number of hurricanes that will hit a certain house in the next ten years is Poisson distributed with mean 4. Each hurricane results in a loss that is exponentially distributed with mean 1000. Losses

Falk Thiele asked Mar 5, 2022

420,231 views

1 Answer

Answer:

The variance of total loss is 8000000

Explanation:

Let

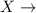$X \to$ Number of hurricane

Poisson
E(X) = 4

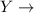$Y \to$ Loss in each hurricane

Exponential
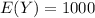
E(Y) = 1000

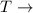$T \to$ Total Loss

Required

The variance of the total loss

This is calculated as:

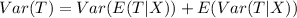
Var(T) = Var(E(T|X)) + E(Var(T|X))

Where:

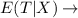$E(T|X) \to$ Expected total loss given X hurricanes

And it is calculated as:

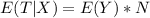E(T|X) = E(Y) *N --- Expected Loss in each hurricane * number of loss

$Var(T|X) \to$ Variance of total loss given X hurricanes

And it is calculated as:

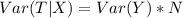Var(T|X) = Var(Y) * N ---- --- Variance of loss in each hurricane * number of loss

So, we have:

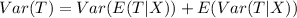
Var(T) = Var(E(T|X)) + E(Var(T|X))

Var(T) = Var(E(Y) * N) + E(Var(Y) * N)

For exponential distribution;

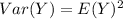
Var(Y) = E(Y)^2

So, we have:

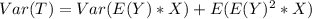
Var(T) = Var(E(Y) * X) + E(E(Y)^2 * X)

Substitute values

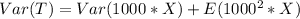
Var(T) = Var(1000 * X) + E(1000^2 * X)

Simplify:

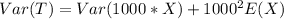
Var(T) = Var(1000 * X) + 1000^2E(X)

Using variance formula, we have:

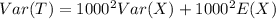
Var(T) = 1000^2Var(X) + 1000^2E(X)

For poission distribution:

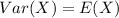
Var(X) = E(X)

So, we have:

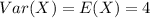
Var(X) = E(X) = 4

The expression becomes:

Var(T) = 1000^2*4 + 1000^2*4

Var(T) = 1000000*4 + 1000000*4

Var(T) = 4000000 + 4000000

Var(T) = 8000000

GauRang Omar answered Mar 12, 2022

by GauRang Omar

3.0k points

Search QAmmunity.org