Question

Determine the resolution of a manometer required to measure the velocity of air at 50 m/s using a pitot-static tube and a manometer fluid of mercury (density: 13,600 kg/m3) to achieve uncertainty of 5% (i.e., 2.5 m/s) and 1 % (0.5 m/s).

Answer 1

a) Δh = 2 cm, b) Δh = 0.4 cm

Step-by-step explanation:

Let's start by using Bernoulli's equation for the Pitot tube, we define two points 1 for the small entry point and point 2 for the larger diameter entry point.

P₁ + ½ ρ v₁² + ρ g y₁ = P₂ + ½ ρ v₂² + ρ g y₂

Point 1 is called the stagnation point where the fluid velocity is reduced to zero (v₁ = 0), in general pitot tubes are used in such a way that the height of point 2 of is the same of point 1

y₁ = y₂

subtitute

P₁ = P₂ + ½ ρ v₂²

P₁ -P₂ = ½ ρ v²

where ρ is the density of fluid

now we measure the pressure on the included beforehand as a pair of communicating tubes filled with mercury, we set our reference system at the point of the mercury bottom surface

ΔP =ρ_{Hg} g h - ρ g h

ΔP = (ρ_{Hg} - ρ) g h

as the static pressure we can equalize the equations

ΔP = P₁ - P₂

(ρ_{Hg} - ρ) g h = ½ ρ v²

v =
`\sqrt{(2 (\rho_(Hg) - \rho) g)/(\rho ) } \ √(h)`

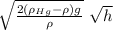
in this expression the densities are constant

v = A √h

A =
`\sqrt{(2(\rho_(Hg) - \rho ) g)/(\rho ) }`

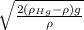
They indicate the density of mercury rhohg = 13600 kg / m³, the density of dry air at 20ºC is rho air = 1.29 kg/m³

we look for the constant

A =
`\sqrt{(2( 13600 - 1.29) \ 9.8)/(1.29) }`

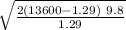
A = 454.55

we substitute

v = 454.55 √h

to calculate the uncertainty or error of the velocity

h =
`(1)/(454.55^2) \ v^2`

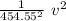
Δh =
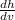`(dh)/(dv)` Δv

`(\Delta h)/(h ) = 2 \ (\Delta v)/(v)`

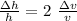
Suppose we have a height reading of h = 20 cm = 0.20 m

a) uncertainty 2.5 m / s ( 0.05)

`(\delta v)/(v) = 0.05`

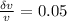
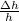`(\Delta h)/(h)` = 2 0.05

Δh = 0.1 h

Δh = 0.1 20 cm

Δh = 2 cm

b) uncertainty 0.5 m / s ( Δv/v= 0.01)

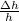`(\Delta h)/(h)` = 2 0.01

Δh = 0.02 h

Δh = 0.02 20

Δh = 0.1 20 cm

Δh = 0.4 cm = 4 mm