Question

Solve the system by substitution. x= 2y + 7 3x – 2y = 3 The solution is?​

Answer 1

Hi there! Your answer is x = -2, y = -9/2

In coordinate point, we can write (-2,-9/2)

Please see the explanation below for a clear understand about the problem.

Any questions about the answer, feel free to ask in comment! :)

Explanation:

Goal

• Solve the system of equations by substitution method.

Given

• System of Equations

`\begin{cases} x=2y+7 \Longrightarrow (1)\\ 3x-2y=3 \Longrightarrow (2) \end{cases}`

Step 1

• Since our x-term is the subject in the first equation, we can simply substitute x = 2y+7 in the second equation.

Substitute x = 2y+7 in the second equation.

`3x-2y=3\\3(2y+7)-2y=3`

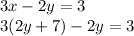
We do this so we can solve for the y-term without any problems. (We need to get rid of a variable if there are more than one variable.)

Then we distribute/expand 3 in the expression.

`6y+21-2y=3\\4y+21=3`

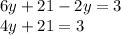
Step 2

• Solve the equation for y-term

To solve the equation, we have to isolate the term that we want. For this scenario, we want to know the value of y-term. Therefore, we isolate y-term.

`4y=3-21\\4y=-18\\y=-(18)/(4) \\y=-(9)/(2)`

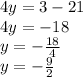
Finally! we know the value of y which is -9/2. But we are not done yet!

Step 3

• Substitute the y-value in any given equations.

After we solve the equation, we have to substitute the value in any given equations. No need to substitute the value in both equations! Choose an equation to substitute the value in.

For this, I will be choosing an equation with less coefficients which is the first equation.

`x=2y+7`

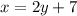
Substitute y = -9/2 in the equation.

`x=2(-(9)/(2))+7\\x=-9+7\\x=-2`

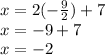
We should get x = -2 as the answer. This is our last step for finding an answer. The next few steps are going to be how to check the answer for system of equations. Note that next few steps are optional. If you are not certain that the answer is wrong or right, it is highly advised to check the answer before jumping to a conclusion!

Optional Steps - Answer Check

To check the answer, we can simply substitute both x-value and y-value in any given equations. You can either choose only a single equation to substitute in ONLY if you are certain/sure that the answer is likely correct. Substituting in both equations are recommended for beginners.

Step 3

• Substitute x = -2 and y = -9/2 in the system of equations.

Step 3.1

• Substitute in x = 2y+7

`x=2y+7`

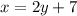
From x = -2 and y = -9/2

`-2=2(-(9)/(2) )+7`

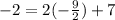
Cancel 2 out.

`-2=-9+7\\-2=-2`

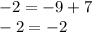
As you can see, both sides are equal. That means the equation is true for x = -2 and y = -9/2.

Step 3.2

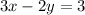
• Substitute in 3x-2y = 3

`3x-2y=3`

Substitute x = -2 and y = -9/2 in the equation.

`3(-2)-2(-(9)/(2))=3\\-6+(18)/(2)=3\\-6+9=3\\3=3`

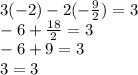
Since both equations are true for x = -2 and y = -9/4. We can conclude that:

`\huge\sf{x = -2 \ and \ y = -(9)/(2) \ are \ the \ solutions \ to \ the \ system \ of \ equations.}`

Hence, the answer is x = -2 and y = -9/2.