Question

For this problem, assume that the committee contains 6 men and 9 women and that three are selected at random for a subcommittee. What is the probability that the subcommittee consists of 2 men and 1 woman, given that it contains both men and women

Answer 1

0.3846 = 38.46% probability that the subcommittee consists of 2 men and 1 woman.

Explanation:

A probability is the number of desired outcomes divided by the number of total outcomes.

To solve this question, we need to know the combinations formula and conditional probability.

Combinations formula:

`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

Conditional Probability

We use the conditional probability formula to solve this question. It is

`P(B|A) = (P(A \cap B))/(P(A))`

In which

P(B|A) is the probability of event B happening, given that A happened.

`P(A \cap B)` is the probability of both A and B happening.

P(A) is the probability of A happening.

What is the probability that the subcommittee consists of 2 men and 1 woman, given that it contains both men and women?

Event A: Contains both men and woman

Event B: Consists of two men and 1 woman.

Probability of containing both men and woman:

Desired outcomes:

2 men(from a set of 6) and 1 woman(from a set of 9), or 1 men(from a set of 6) and 2 women(from a set of 9). So

`D = C_(6,2)*C_(9,1) + C_(6,1)*C_(9,2) = (6!)/(2!4!)*(9!)/(1!8!) + (6!)/(1!5!)*(9!)/(2!7!) = 351`

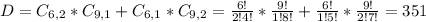
Total outcomes:

3 people from a set of 6 + 9 = 15. So

`T = (15!)/(3!12!) = 455`

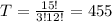
Probability:

`P(A) = (D)/(T) = (351)/(455) = 0.7714`

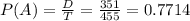
Intersection of events A and B:

Intersection between both men and women, and 2 men and 1 woman, is 2 man and 1 women. So

Desired outcomes:

2 men(from a set of 6) and 1 woman(from a set of 9).

`D = C_(6,2)*C_(9,1) = 135`

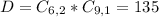
Total outcomes:

3 people from a set of 6 + 9 = 15. So

`T = (15!)/(3!12!) = 455`

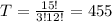
Probability:

`P(A \cap B) = (D)/(T) = (135)/(455) = 0.2967`

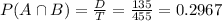
Desired probability:

`P(B|A) = (P(A \cap B))/(P(A)) = (0.2967)/(0.7714) = 0.3846`

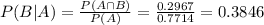
0.3846 = 38.46% probability that the subcommittee consists of 2 men and 1 woman.