Question

Find p(-2) if p(x)=3x^3 -x^2 +2x-5. What does this tell you about the factors of p(x)

Answer 1

`\boxed{\textsf{ The value of the polynomial at p = (-2) is \textbf{ -37}.}}`

Explanation:

A polynomial is given to us and we need to find its value at p = (-2) . The given polynomial is :-

`\sf\implies p(x)= 3x^3 -x^2 +2x-5`

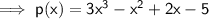
Also second part of the question says what does this tell about the factors of p(x) .

On putting p = (-2) :-

`\sf \implies p(x)= 3x^3 -x^2 +2x-5 \\\\\sf\implies p(-2) = 3 (-2)^3-(-2)^2+2(-2)-5 \\\\\sf\implies p(-2)= 3* (-8) -4 -4 -5 \\\\\sf\implies p(-2)=-24-4-4-5 \\\\\implies \boxed{ \pink{\sf p(-2)= (-37) }}`

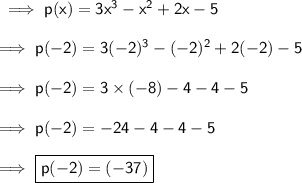
Now this tells us that ( x + 2 ) is not a factor of the given polynomial. When we divide the given polynomial by (x + 2) then the remainder will be -37 .