Answer:
a) The reorder point necessary to provide a 95 percent service probability is 1557 units.
b) The Z value of 0.74 corresponds to 77% service probability.
Explanation:
Average weekly demand (d) = 315 units
The standard deviation of weekly demand (\sigmad) = 90 units
Lead time (L) = 4 weeks
At 95% service level value of Z = 1.65
Reorder point = d x L + safety stock
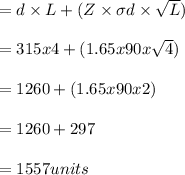
b) Earlier the safety stock was 297 units(calculated in part a)
Now the safety stock is reduced to 55%.so,55% of 297 = 163.35 units
So the new safety stock = 297 - 163.35 = 133.65
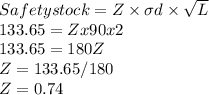
The Z value of 0.74 corresponds to 77% service probability.