Answer:
The time of motion is 333.3 s
The angular acceleration is -0.0045 rad/s²
Step-by-step explanation:
Given;
angular distance of the flywheel, θ = 40 rev
initial angular speed,
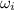 = 1.5 rad/s
= 1.5 rad/s
When the wheel comes to rest, the final angular speed,
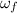 = 0
= 0
The angular acceleration is calculated as follows;
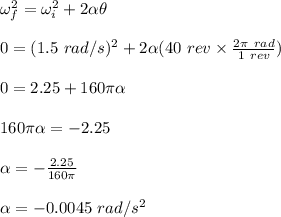
The time of motion is calculated as;
