Answer:
(a) Residents
(b)

(c)
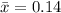
(d) Right skewed
Explanation:
Given
The data of residents without health insurance
Solving (a): The variable
The variable is the residents
Solving (b): The median
First, we sort the data
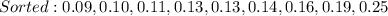
So, the median position is:
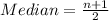
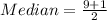

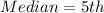
The 5th element of the dataset is: 0.13
So:

Solving (c): The mean
This is calculated as:
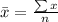
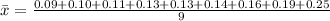
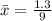
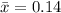
Solving (d): The shape of the distribution
In (b) and (c), we have:

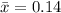
By comparison, the mean is greater than the median.
Hence, the shape is: right skewed.