Question

Steam at 4 MPa and 350°C is expanded in an adiabatic turbine to 125kPa. What is the isentropic efficiency (percent) of this turbine if the steam is exhausted as a saturated vapor?

Answer 1

`\eta_(turbine) = 0.603 = 60.3\%`

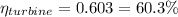
Step-by-step explanation:

First, we will find actual properties at given inlet and outlet states by the use of steam tables:

AT INLET:

At 4MPa and 350°C, from the superheated table:

h₁ = 3093.3 KJ/kg

s₁ = 6.5843 KJ/kg.K

AT OUTLET:

At P₂ = 125 KPa and steam is saturated in vapor state:

h₂ =
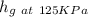`h_(g\ at\ 125KPa)` = 2684.9 KJ/kg

Now, for the isentropic enthalpy, we have:

P₂ = 125 KPa and s₂ = s₁ = 6.5843 KJ/kg.K

Since s₂ is less than
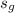`s_g` and greater than
`s_f` at 125 KPa. Therefore, the steam is in a saturated mixture state. So:

`x = (s_2-s_f)/(s_(fg)) \\\\x = (6.5843\ KJ/kg.K - 1.3741\ KJ/kg.K)/(5.91\ KJ/kg.K)\\\\x = 0.88`

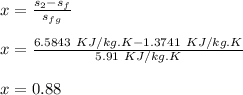
Now, we will find
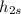`h_(2s)`(enthalpy at the outlet for the isentropic process):

`h_(2s) = h_(f\ at\ 125KPa)+xh_(fg\ at\ 125KPa)\\\\h_(2s) = 444.36\ KJ/kg + (0.88)(2240.6\ KJ/kg)\\h_(2s) = 2416.088\ KJ/kg`

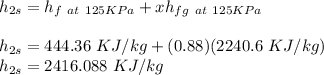
Now, the isentropic efficiency of the turbine can be given as follows:

`\eta_(turbine) = (h_1-h_2)/(h_1-h_(2s))\\\\\eta_(turbine) = (3093.3\ KJ/kg-2684.9\ KJ/kg)/(3093.3\ KJ/kg-2416.088\ KJ/kg)\\\\\eta_(turbine) = (408.4\ KJ/kg)/(677.212\ KJ/kg)\\\\\eta_(turbine) = 0.603 = 60.3\%`