Answer:
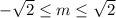 would ensure that at least one real root exists for this equation when solving for
would ensure that at least one real root exists for this equation when solving for
 .
.
Explanation:
Apply the Pythagorean identity
 to replace the cosine this equation with sine:
to replace the cosine this equation with sine:
 .
.
Multiply both sides by
 to obtain:
to obtain:
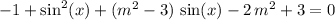 .
.
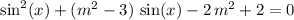 .
.
If
 , then this equation would become a quadratic equation about
, then this equation would become a quadratic equation about
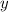 :
:
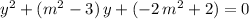 .
.
However,
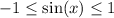 for all real
for all real
 .
.
Hence, the value of
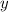 must be between
must be between
 and
and
 (inclusive) for the original equation to have a real root when solving for
(inclusive) for the original equation to have a real root when solving for
 .
.
Determinant of this quadratic equation about
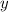 :
:
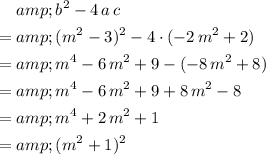 .
.
Hence, when solving for
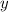 , the roots of
, the roots of
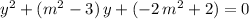 in terms of
in terms of
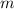 would be:
would be:
 .
.
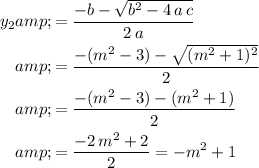 .
.
Since
 , it is necessary that
, it is necessary that
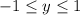 for the original solution to have a real root when solved for
for the original solution to have a real root when solved for
 .
.
The first solution,
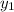 , does not meet the requirements. On the other hand, simplifying
, does not meet the requirements. On the other hand, simplifying
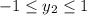 ,
,
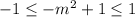 gives:
gives:
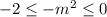 .
.
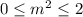 .
.
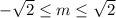 .
.
In other words, solving
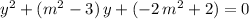 for
for
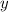 would give a real root between
would give a real root between
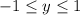 if and only if
if and only if
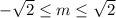 .
.
On the other hand, given that
 for the
for the
 in the original equation, solving that equation for
in the original equation, solving that equation for
 would give a real root if and only if
would give a real root if and only if
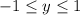 .
.
Therefore, the original equation with
 as the unknown has a real root if and only if
as the unknown has a real root if and only if
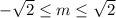 .
.