Question

A claim is made that the proportion of 6-10 year-old children who play sports is not equal to 0.5. A

random sample of 551 children aged 6-10 showed that 48% of them play a sport.
For each part below, enter only a numeric value in the answer box. For example, do not type "z =" or "t="
before your answers. Round each of your answers to 3 places after the decimal point.
(a) Calculate the value of the test statistic used in this test.
Test statistic's value
(b) Use your calculator to find the P-value of this test.
P-value =
(c) Use your calculator to find the critical value(s) used to test this claim at the 0.02 significance level. If
there are two critical values, then list them both with a comma between them.
Critical value(s) -

Answer 1

a) -0.94

b) 0.3472

c) -2.327, 2.327

Explanation:

A claim is made that the proportion of 6-10 year-old children who play sports is not equal to 0.5.

At the null hypothesis, we test if the proportion is of 0.5, that is:

`H_0: p = 0.5`

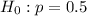
At the alternative hypothesis, we test if the proportion is different from 0.5, that is:

`H_1: p \\eq 0.5`

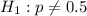
The test statistic is:

`z = (X - \mu)/((\sigma)/(√(n)))`

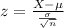
In which X is the sample mean,
`\mu` is the value tested at the null hypothesis,
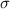`\sigma` is the standard deviation and n is the size of the sample.

0.5 is tested at the null hypothesis:

This means that
`\mu = 0.5, \sigma = √(0.5*(1-0.5)) = 0.5`

A random sample of 551 children aged 6-10 showed that 48% of them play a sport.

This means that
`n = 551, X = 0.48`

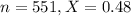
(a) Calculate the value of the test statistic used in this test.

`z = (X - \mu)/((\sigma)/(√(n)))`

`z = (0.48 - 0.5)/((0.5)/(√(551)))`

`z = -0.94`

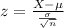
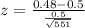
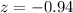
So the answer is -0.94.

(b) Use your calculator to find the P-value of this test.

The p-value of the test is the probability that the sample proportion differs from 0.5 by at least 0.02, which is P(|z| > 0.94), which is 2 multiplied by the p-value of Z = -0.94.

Looking at the z-table, z = -0.94 has a p-value of 0.1736.

2*0.1736 = 0.3472, so 0.3472 is the answer to option b.

(c) Use your calculator to find the critical value(s) used to test this claim at the 0.02 significance level.

Two-tailed test(test if the mean differs from a value), Z with a p-value of 0.02/2 = 0.01 or 1 - 0.01 = 0.99.

Looking at the z-table, this is z = -2.327 or z = 2.327.