Question

The graph of F(x) can be compressed vertically and shifted to the right to produce the graph of G(x) . If F(x) = x ^ 3 , which of the following could be the equation of G(x) ?

Answer 1

Given:

The function is:

`F(x)=x^3`

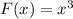
To find:

The function G(x) if the graph of F(x) can be compressed vertically and shifted to the right to produce the graph of G(x).

Solution:

The transformation is defined as

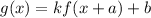`g(x)=kf(x+a)+b` .... (i)

Where, k is stretch factor, a is horizontal shift and b is vertical shift.

If 0<k<1, then the graph compressed vertically by factor k and if k>1, then the graph stretch vertically by factor k.

If a>0, then the graph shifts a units left and if a<0, then the graph shifts a units right.

If b>0, then the graph shifts b units up and if b<0, then the graph shifts b units down.

It is given that F(x) can be compressed vertically and shifted to the right to produce the graph of G(x). So, the value of k must be lies between 0 and 1, and a<0.

In option A,
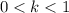`0<k<1` and
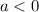`a<0`. So, this option is correct.

In option B,
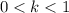`0<k<1` and
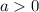`a>0`. So, this option is incorrect.

In option C,
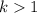`k>1` and
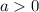`a>0`. So, this option is incorrect.

In option D,
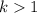`k>1` and
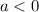`a<0`. So, this option is incorrect.

Therefore, the correct option is A.