Sum of three consecutive odd integers =
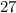

The values of the three integers.

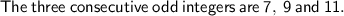

Let us assume the three consecutive odd integers to be
 ,
,
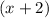 and
and
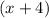 .
.
As per the condition, we have
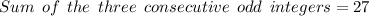
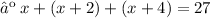
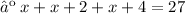
Now, collect the like terms.
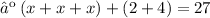
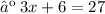
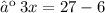
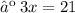
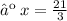
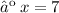
Therefore, the three consecutive odd integers whose sum is
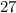 are
are
 ,
,
 and
and
 respectively.
respectively.

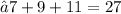
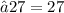
⇢ L. H. S. = R. H. S.