Question

4. The average salary for public school teachers for a specific year was reported to be $39,385. A random sample of 50 public school teachers in a particular state had a mean of $41,680, and the population standard deviation is $5975. Is there sufficient evidence at the a _ 0.05 level to conclude that the mean salary differs from $39,385

Answer 1

The p-value of the test is 0.0066 < 0.05, which means that there is sufficient evidence at the 0.05 significance level to conclude that the mean salary differs from $39,385

Explanation:

The average salary for public school teachers for a specific year was reported to be $39,385. Test if the mean salary differs from $39,385

At the null hypothesis, we test if the mean is of $39,385, that is:

`H_0: \mu = 39385`

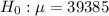
At the alternative hypothesis, we test if the mean differs from this, that is:

`H_1: \mu \\eq 39385`

The test statistic is:

`z = (X - \mu)/((\sigma)/(√(n)))`

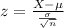
In which X is the sample mean,
`\mu` is the value tested at the null hypothesis,
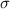`\sigma` is the standard deviation and n is the size of the sample.

39385 is tested at the null hypothesis:

This means that
`\mu = 39385`

A random sample of 50 public school teachers in a particular state had a mean of $41,680, and the population standard deviation is $5975.

This means that
`n = 50, X = 41680, \sigma = 5975`

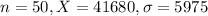
Value of the test statistic:

`z = (X - \mu)/((\sigma)/(√(n)))`

`z = (41680 - 39385)/((5975)/(√(50)))`

`z = 2.72`

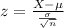
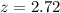
P-value of the test and decision:

The p-value of the test is the probability that the sample mean differs from 39385 by at least 2295, which is P(|Z| > 2.72), which is 2 multiplied by the p-value of Z = -2.72.

Looking at the z-table, Z = -2.72 has a p-value of 0.0033

2*0.0033 = 0.0066

The p-value of the test is 0.0066 < 0.05, which means that there is sufficient evidence at the 0.05 significance level to conclude that the mean salary differs from $39,385