Question

g A 0.750-kg ball traveling horizontally on a frictionless surface approaches a very massive stone at 20.0 m/s perpendicular to wall and rebounds with 70.0% of its initial kinetic energy. What is the magnitude of the change in momentum of the stone

Answer 1

v = 1.23 m / s

the stone goes in the initial direction of the ball.

Step-by-step explanation:

This is a momentum conservation problem, they indicate that after the crash its speed is 70% of its initial energy.

K_f = 0.7 K₀

½ m v_f² = 0.7 ½ m v₀²

v_f² = 0.7 v₀²

v_f = √0.7 v₀

v_f = √0.7 20

v_f = 16.73 m / s

now we can use conservation the moment

initial instant. Before the crash

p₀ = m v₀ + 0

final instant. After the crash

p_f = m v_f + M v

p₀ = p_f

m v₀ = m v_f + M v

v =
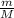`( m)/( M)` (v₀ - v_f)

v = 0.750 (20 - 16.73) / M

v = 2.4525 / M

To finish the exercise we must assume a mass of the stone, generally higher than the mass of the ball.

M = 2 kg

v = 2.4525 / 2

v = 1.23 m / s

the stone goes in the initial direction of the ball.