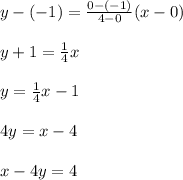Question

A coordinate plane with a line passing through the points (0, negative 1, 0) and (4, 0).

What is the equation of the graphed line written in standard form?

x – 4y = 4
x + 4y = 4
y = y equals StartFraction one-fourth EndFraction x minus 1.x – 1
y = –y equals negative StartFraction one-fourth EndFraction x minus 1.x – 1

Answer 1

Explanation:

Answer 2

x-4y=4

Explanation:

The equation of a straight line is in slope intercept form:

y = mx + b;

where y and x are variables, m is the slope of the line and b is the y intercept.

The standard form of a line is:

Ax + By = C

where A, B and C are constants, x and y are variables

The equation of a straight line passing through the points (x₁, y₁) and (x₂, y₂) is given by:

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)\\`

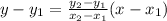
Given that a line passes through the points (0, -1) and (4, 0), the equation of the line is given by:

`y-(-1)=(0-(-1))/(4-0) (x-0)\\\\y+1=(1)/(4) x\\\\y=(1)/(4) x-1\\\\4y=x-4\\\\x-4y=4`