Question

Find the area of the region in two ways. a. Using integration with respect to x. b. Using geometry. 9-x

Answer 1

Answer: hello your question is incomplete attached below is the complete question

answer :

a)
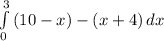`\int\limits^3_0 {(10-x)-(x+4)} \, dx` ( option D )

b) A = 1/2 (6)(3) ( option B )

c) Area of shaded region = 9

Explanation:

a) Using integration with respect to x

Area =
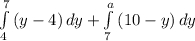`\int\limits^7_4 {(y-4)} \, dy + \int\limits^a_7 {(10-y)} \, dy` ( note a = 10 )

= y^2/2 - 4y |⁷₄ + 10y - y^2/2 |¹⁰₇

= 33/2 - 12 + 30 - 51/2 = 9

hence the best integral from the options attached is option D

`\int\limits^3_0 {(10-x)-(x+4)} \, dx`

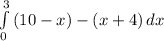
= [ 10x - x^2 /2 - x^2/2 - 9x ] ³₀

= 30 - 9/2 - 9/2 - 12 = 9

b) Using Geometry

Area = 1/2 * base * height

= 1/2 * 6 * 3

= 9