Question

Three forces are applied to a solid cylinder of mass 12 kg (see the drawing). The magnitudes of the forces are F1 = 15 N, F2 = 24 N, and F3 = 13 N. The radial distances are R2 = 0.22 m and R3 = 0.10 m. The forces F2 and F3 are perpendicular to the radial lines labeled R2 and R3. The moment of inertia of the cylinder is 1/2 MR 2/2. Find the magnitude of the angular acceleration of the cylinder about the axis of rotation.

Answer 1

α = 13.7 rad / s²

Step-by-step explanation:

Let's use Newton's second law for rotational motion

∑ τ = I α

we will assume that the counterclockwise turns are positive

F₁ 0 + F₂ R₂ - F₃ R₃ = I α

give us the cylinder moment of inertia

I = ½ M R₂²

α = (F₂ R₂ - F₃ R₃)
`(2)/(M R_2^2)`

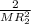
let's calculate

α = (24 0.22 - 13 0.10)
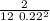`(2)/(12 \ 0.22^2)`2/12 0.22²

α = 13.7 rad / s²