Question

A concession stand at an athletic event is trying to determine how much to sell cola and iced tea for in order to maximize revenue. Let x be the price per cola and y the price per iced tea. Demand for cola is 100 – 34x + 5y colas per game and iced tea is 50 + 3x – 16y iced teas per game The concession stand should charge: dollars per cola, dollars per iced tea, in order to maximize revenue. The maximum revenue for one game is: dollars.

Answer 1

Demand for cola : 100 – 34x + 5y

Demand for cola : 50 + 3x – 16y

Therefore, total revenue :

x(100 – 34x + 5y) + y(50 + 3x – 16y)

R(x,y) =
`$100x-34x^2+5xy+50y+3xy-16y^2$`

`$R(x,y) = 100x-34x^2+8xy+50y-16y^2$`

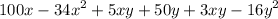
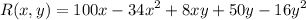
In order to maximize the revenue, set

`$R_x=0, \ \ \ R_y=0$`

`$R_x=(dR )/(dx) = 100-68x+8y$`

`$R_x=0$`

`$68x-8y=100$` .............(i)

`$R_y=(dR )/(dx) = 50-32x+8y$`

`$R_y=0$`

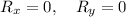
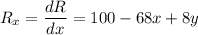
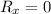
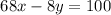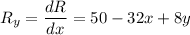
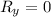
`$8x-32y=-50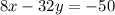$` .............(ii)

Solving (i) and (ii),

4 x (i) ⇒ 272x - 32y = 400

(ii) ⇒ (-) 8x - 32y = -50

264x = 450

∴
`$x=(450)/(264)=(75)/(44)$`

`$y=(175)/(88)$`

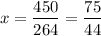
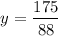
So, x ≈ $ 1.70 and y = $ 1.99

R(1.70, 1.99) = $ 134.94

Thus, 1.70 dollars per cola

1.99 dollars per iced ted to maximize the revenue.

Maximum revenue = $ 134.94