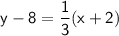Answer:
5. Slope-intercept form:
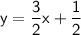
6. Point-slope form:
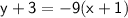
7. Point-slope form:
Explanation:
5. To find the slope of the line, we use the following formula:

where
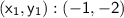 and
and
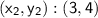 are two points on the line.
are two points on the line.
In this case, we have:
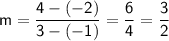
Therefore, the slope of the line is 3/2.
To find the y-intercept, we can substitute one of the points into the slope-intercept form of the equation of a line:
y = mx + b
Substituting (-1, -2) into the equation, we get:
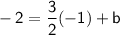
Solving for b, we get:
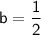
Therefore, the equation of the line in slope-intercept form is:
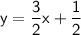
6. To find the equation of the line in point-slope form, we use the following formula:
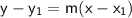
where
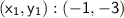 is a point on the line and m is the slope of the line(m) = -9.
is a point on the line and m is the slope of the line(m) = -9.
In this case, we have:

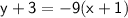
Therefore, the equation of the line in point-slope form is:
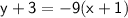
7. To find the equation of the line in point-slope form, we use the same formula as in the previous problem.
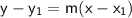
where
 is a point on the line and m is the slope of the line(m) = 1/3.
is a point on the line and m is the slope of the line(m) = 1/3.
In this case, we have:
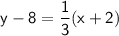
Therefore, the equation of the line in point-slope form is: