Question

Difference Quotient. Correct answer is shown. It says multiply by conjugate but I don’t understand what that is and how they did it. TIA

Answer 1

9514 1404 393

Answer:

3/(√(3(x+h)) +√(3x))

Explanation:

The conjugate of a binomial is the same sum, but with the sign changed. That is (a +b) and (a -b) are a conjugate pair: each is the conjugate of the other.

The purpose of multiplying expressions involving roots or complex numbers by their conjugate is to take advantage of the relation ...

(a +b)(a -b) = a² -b²

Here. you want to eliminate the h from under the radical, so squaring the radical containing h is useful for the purpose. Hence the conjugate gets involved.

"Multiply by the conjugate" means multiply both the numerator and the denominator by the conjugate. (Effectively, multiply by 1.)

__

`\displaystyle(f(x+h)-f(x))/(h)=(√(3(x+h))-√(3x))/(h)\\\\=((√(3(x+h))-√(3x))(√(3(x+h))+√(3x)))/(h(√(3(x+h))+√(3x)))=(3(x+h)-3x)/(h(√(3(x+h))+√(3x)))\\\\=(3h)/(h(√(3(x+h))+√(3x)))=\boxed{(3)/(√(3(x+h))+√(3x))}`

_____

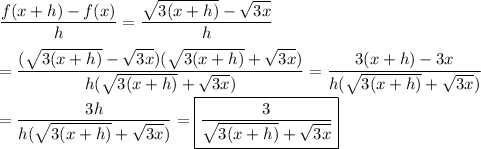
Additional comment

In the end, you will want the limit as h → 0, which will be 3/(2√(3x)). You will notice that h=0 no longer makes the denominator zero, so the limit is found by simple evaluation.

When the "binomial" is a complex number of the form a+bi, its conjugate is a-bi, regardless of the sign of b. That is, the conjugate of a complex number is found by negating its imaginary part. The sign of the real part is left alone.