Question

Find the area of the triangle with the given base and height.
b = 3 m and h = 10 1/2 m

Answer 1

Area of triangle =
`\boxed{\sf{15(3)/(4)}}` m².

Step-by-step Step-by-step explanation:

Here's the required formula to find the area of triangle :

`\longrightarrow{\pmb{\sf{Area_((\triangle)) = (1)/(2) * b * h}}}`

• △ = triangle
• b = base
• h = height

Substituting all the given values in the formula to find the area of triangle :

`\twoheadrightarrow{\sf{Area_((\triangle)) = (1)/(2) * b * h}}`

`\twoheadrightarrow{\sf{Area_((\triangle)) = (1)/(2) * 3 * 10 (1)/(2)}}`

`\twoheadrightarrow{\sf{Area_((\triangle)) = (1)/(2) * 3 * (20 + 1)/(2)}}`

`\twoheadrightarrow{\sf{Area_((\triangle)) = (1)/(2) * 3 * (21)/(2)}}`

`\twoheadrightarrow{\sf{Area_((\triangle)) = (1 * 3 * 21)/(2 * 2)}}`

`\twoheadrightarrow{\sf{Area_((\triangle)) = (3 * 21)/(2 * 2)}}`

`\twoheadrightarrow{\sf{Area_((\triangle)) = (63)/(4) \: {m}^(2) }}`

`\twoheadrightarrow{\sf{Area_((\triangle)) = 15(3)/(4) \: {m}^(2) }}`

`\star{\underline{\boxed{\sf{\red{Area_((\triangle)) = 15(3)/(4) \: {m}^(2)}}}}}`

Hence, the area of triangle is
`\bf{15(3)/(4)}` m².

`\rule{300}{2.5}`

Answer 2

Statement:

The base of a triangle is 3m and its height is
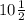`10 (1)/(2)` m.

To find out:

The area of the triangle.

Solution:

• Given, base = 3m, height =
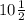  `10 (1)/(2)`m
• We know,

`\sf \: area \: \: of \: \: a \: \: triangle = (1)/(2) * base \: * height`

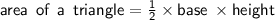
• Therefore, the area of the triangle

`\sf = ((1)/(2) * 3 * 10 (1)/(2) ) {m}^(2) \\ \sf = ( (1)/(2) * 3 * (21)/(2) ) {m}^(2) \\ = \sf (63)/(4) {m}^(2) \\ = \sf 15(3)/(4) {m}^(2)`

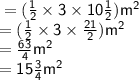
Answer:

The area of the triangle is
`\sf \: 15 (3)/(4) {m}^(2)`

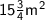
Hope you could understand.

If you have any query, feel free to ask.