Question

A 0.150 kg stone rests on a frictionless, horizontal surface. A bullet of mass 9.50 g, traveling horizontally at 380 m/s, strikes the stone and rebounds horizontally at right angles to its original direction with a speed of 250 m/s.

Required:
a. Compute the magnitude and direction of the velocity of the stone after it is struck.
b. Is the collision perfectly elastic?

Answer 1

(a)Magnitude=28.81 m/s

Direction=33.3 degree below the horizontal

(b) No, it is not perfectly elastic collision

Step-by-step explanation:

We are given that

Mass of stone, M=0.150 kg

Mass of bullet, m=9.50 g=
`9.50* 10^(3) kg`

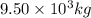
Initial speed of bullet, u=380 m/s

Initial speed of stone, U=0

Final speed of bullet, v=250m/s

a. We have to find the magnitude and direction of the velocity of the stone after it is struck.

Using conservation of momentum

`mu+ MU=mv+ MV`

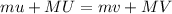
Substitute the values

`9.5* 10^(-3)* 380 i+0.150(0)=9.5* 10^(-3) (250)j+0.150V`

`3.61i=2.375j+0.150V`

`3.61 i-2.375j=0.150V`

`V=(1)/(0.150)(3.61 i-2.375j)`

`V=24.07i-15.83j`

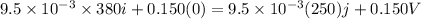
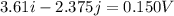
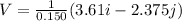
Magnitude of velocity of stone

=
`√((24.07)^2+(-15.83)^2)`

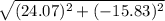
|V|=28.81 m/s

Hence, the magnitude and direction of the velocity of the stone after it is struck, |V|=28.81 m/s

Direction

`\theta=tan^(-1)((y)/(x))`

=
`tan^(-1)((-15.83)/(24.07))`

`\theta=tan^(-1)(-0.657)`

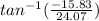
=33.3 degree below the horizontal

(b)

Initial kinetic energy

`K_i=(1)/(2)mu^2+0=(1)/(2)(9.5* 10^(-3))(380)^2`

`K_i=685.9 J`

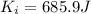
Final kinetic energy

`K_f=(1)/(2)mv^2+(1)/(2)MV^2`

=
`(1)/(2)(9.5* 10^(-3))(250)^2+(1)/(2)(0.150)(28.81)^2`

`K_f=359.12 J`

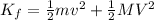
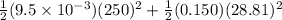
Initial kinetic energy is not equal to final kinetic energy. Hence, the collision is not perfectly elastic collision.