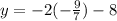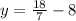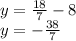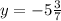Question

Help----------------------------

Answer 1

One solution;

`x=-1(2)/(7)`

`y=-5(3)/(7)`

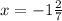
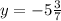
Explanation:

The method of elimination is a way of solving a system of equations. There are many steps involved in this process. First, one must manipulate one of the equations in the system by multiplying each term in it by a certain number such that one of the variables is the inverse of the other like the variable in the other equation. Then one must add the two equations. This will eliminate one of the variables in the equations. After doing so, one has to use inverse operations to solve for the other variable. Finally, one will back solve, substitute the value of the solved variable into one of the equations and solve for the remaining unknown variable.

`\left \{ {{y=5x+1} \atop {y=-2x-8}} \right.`

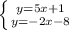
Manipulate the system;

`\left \{ {{y=5x+1*(-1)} \atop {y=-2x-8}} \right.`

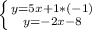
Simplify,

`\left \{ {{-y=-5x-1} \atop {y=-2x-8}} \right.`

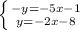
Add the equations,

`\left \{ {{-y=-5x-1} \atop {y=-2x-8}} \right.`

`0=-7x-9`

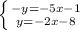
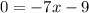
Inverse operations,

`0=-7x-9`

`7x=-9`

`x=-(9)/(7)`

`x=-1(2)/(7)`

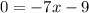
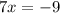
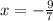
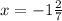
Backsolve,

`y=-2x-8`

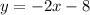
Substitute

`y=-2(-(9)/(7))-8`

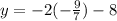
Simplify,

`y=-2(-(9)/(7))-8`

`y=(18)/(7)-8`

`y=(18)/(7)-8\\y=-(38)/(7)`

`y=-5(3)/(7)`