Question

Determine whether the sets are equal, equivalent, both, or neither. {56, 48, 7} and {48, 7, 56}

Answer 1

Answer: Both

Step-by-step explanation

• Equal sets: Two sets that have the same number of items, and the same exact items (perhaps just in a different order)
• Equivalent set: Two sets that have the same number of items, aka same cardinality, but the items themselves are different.

If two sets are equal, then they are automatically equivalent. But not the other way around.

The sets {56, 48, 7} and {48, 7, 56} are equal because they both have 7, 48, and 56 and nothing else. Also, both have the same number of values aka same cardinality. This is why we conclude the final answer is both.

Here's an example of two equivalent sets that aren't equal: {1,2,3} and {4,5,6}. Both have the same cardinality which makes them equivalent sets, but they aren't equal since each set has completely different values.

Put another way: sets A and B are equivalent if and only if n(A) = n(B). The notation "n" refers to the number of items in a set.

Sets A and B are equal if and only if n(A) = n(B) and also
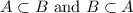`A \subset B \text{ and } B \subset A`; meaning each set is a subset of each other, and hence we can conclude A = B.