Answer:
θ = 12.5 rotations
Step-by-step explanation:
The number of rotations can be found by using the second equation of motion:
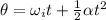
where,
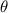 = angular displacement = ?
= angular displacement = ?
ωi = initial angular speed = 0 rad/s
t = time = 5 s
α = angular acceleration = 2π rad/s²
Therefore,

converting it to no. or rotations:

θ = 12.5 rotations