Question

Helppppppppppp:)))))))))

Answer 1

Hi there!

We are given the set of ordered pairs below:

`\large \boxed{(3, - 1),(2, - 2),(0,2),(2,1)}`

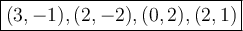
1. What is the domain?

• Domain is a set of all x-values in one set of ordered pairs. So what are the x-values that I am talking about? In ordered pairs, we define x and y which both have relation to each others which we can write as (x,y). That's right, the domain is set of all x-values from ordered pairs.

Therefore, we gather only x-values from (x,y). Hence, the domain is {3,2,0,2}. Whoops! Something is not right. As we learn in Set Theory that we don't write the same or repetitive in a set. Hence, the actual domain is {0,2,3}

2. What is the range?

• Because domain is set of all x-values. Then what do you think the range is? That's right! The range is set of all y-values. If you got this right before looking up the underlined words then a handclap for you! So how do we find range? Simple, we just do like finding the domain in the Q1, except we gather the y-values in (x,y) instead and make sure that we don't write same number!

Therefore, gather y-values from the ordered pairs. Hence, the range is {-2,-1,1,2}

3. Is the relation a function?

• All functions are relations but not all relations are functions. Function is a set of ordered pairs where domain is not repetitive or in a set, there cannot be more than one same value. Consider the following relation: (1,1),(1,2) - Oh, looks like in a set of ordered pairs, there are two same domains which make it only a relation, and not a function. On the other hand, (1,1),(2,2) - Looking good! No same or repetitive domain, making it indeed a function.

Consider the domain from Q1 and see if there are two same values of x in a set. Looks like the relation is not a function since there are same x-values which are 2 in a set, making it only a relation. Hence, the relation is not a function.

These are all 3 answers along with an explanation. Let me know if you have any doubts regarding Relations and Functions.

From the Q1's answer, there are two bold texts, please choose the second bold text to answer (the one with underline) and not the first one (the one with same 2's).

Good luck on your assignment, have a nice day!