Question

If 1/a+1/b+1/c=1/a+b+c then prove that 1/a^9+1/b^9+1/c^9=1/a^9+1/b^9+1/c^9​

Answer 1

The given relation is presented as follows;

`(1)/(a) + (1)/(b) +(1)/(c) = (1)/(a + b + c)`

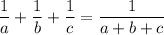
Where 'a', 'b', and 'c' are member of real numbers, we have;

a⁹, b⁹, and c⁹ are also member of real numbers

When a⁹ = x, b⁹ = y, and c⁹ = z

By the above relationship, we have;

`(1)/(x) + (1)/(y) +(1)/(z) = (1)/(x + y + z)`

Substituting x = a⁹, y = b⁹, and z = c⁹, we get;

`(1)/(a^9) + (1)/(b^9) +(1)/(c^9) = (1)/(a^9 + b^9 + c^9)`

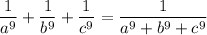
Explanation: