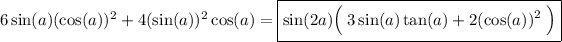Question

D. 2 sin a cos a (3 cos a + 2 sin a) find the product of:​

Answer 1

`\sin(2a)\!\left(\frac{}{}3\sin(a)\tan(a) + 2(\cos(a))^2\frac{}{}\right)`

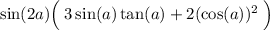
Explanation:

We can find the product of the expression:

`2\sin(a) \cos(a) \cdot \left(\frac{}{}3 \cos(a) + 2\sin(a)\frac{}{}\right)`

by applying the distributive property:

`a(b + c) = ab + ac`

Applying this property, the expression becomes:

`\left(\frac{}{}2\sin(a)\cos(a)\cdot 3\cos(a)\frac{}{}\right) + \left(\frac{}{}2\sin(a)\cos(a) \cdot 2\sin(a)\frac{}{}\right)`

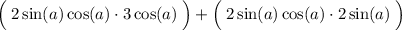
We can simplify this by representing the trigonometric functions multiplied by themselves exponentially:

`6\sin(a)(\cos(a))^2 + 4(\sin(a))^2\cos(a)`

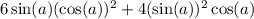
And this can be simplified further using the double angle identity for the sine function:

`\sin(2a) = 2\sin(a)\cos(a)`

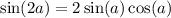
Hence,

`6\sin(a)(\cos(a))^2 + 4(\sin(a))^2\cos(a) = \boxed{\sin(2a)\!\left(\frac{}{}3\sin(a)\tan(a) + 2(\cos(a))^2\frac{}{}\right)}`