Question

Find the time required for an investment of 7,000 dollars to grow to 14,000 dollars at an interest rate of 4% per

year, compounded monthly. Give your answer accurate to 2 decimal places.
Preview
years.

Answer 1

The time required is of 17.53 years.

Explanation:

Compound interest:

The compound interest formula is given by:

`A(t) = P(1 + (r)/(n))^(nt)`

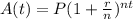
Where A(t) is the amount of money after t years, P is the principal(the initial sum of money), r is the interest rate(as a decimal value), n is the number of times that interest is compounded per year and t is the time in years for which the money is invested or borrowed.

Find the time required for an investment of 7,000 dollars to grow to 14,000 dollars at an interest rate of 4% per year, compounded monthly.

This is t for which
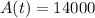`A(t) = 14000`, considering
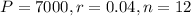`P = 7000, r = 0.04, n = 12`. So

`A(t) = P(1 + (r)/(n))^(nt)`

`14000 = 7000(1 + (0.04)/(12))^(12t)`

`(1.0033)^(12t) = 2`

`\log{(1.0033)^(12t)} = \log{2}`

`12t\log{1.0033} = \log{2}`

`t = \frac{\log{2}}{12\log{1.0033}}`

`t = 17.53`

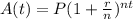
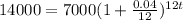
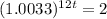
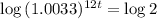
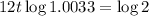
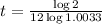
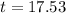
The time required is of 17.53 years.