Question

HELP!!! GIVING OUT 50 POINTS

QUESTION ON BINOMIAL THEOREMS

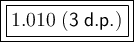
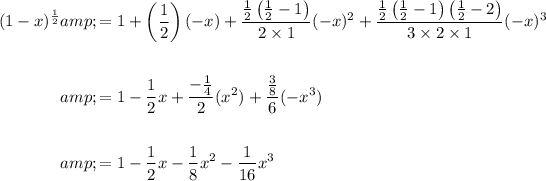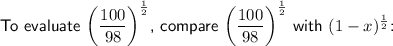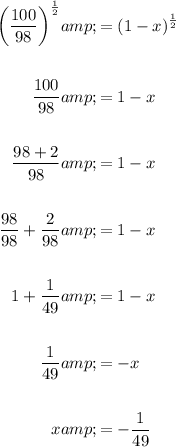Answer 1

`(1-x)^{(1)/(2)} =1-(1)/(2)x-(1)/(8)x^2-(1)/(16)x^3`

`\left((100)/(98)\right)^{(1)/(2)}=1.010\;\sf(3\;d.p.)`

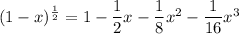
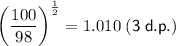
Explanation:

To expand
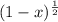`(1-x)^{(1)/(2)` in ascending powers of x up to the fourth term, we can use the binomial series expansion.

The binomial series expansion for (1 + x)ⁿ is given by:

`\boxed{\begin{array}{l}\underline{\sf Binomial\;series}\\\\(1+x)^n=1+nx+(n(n-1))/(1 * 2)x^2+...+(n(n-1)...(n-r+1))/(1 * 2 * ... * r)x^r+...\\\\(|x| < 1, n \in \mathbb{R})\end{array}}`

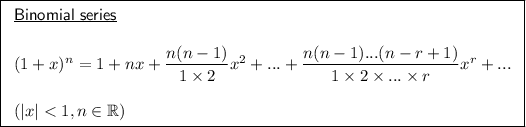
In this case, we have:

• 
  `n=(1)/(2)`

• 
  `x = -x`

Substitute the values into the expansion (to the fourth term) and simplify:

`\begin{aligned}(1-x)^{(1)/(2)} &= 1+\left((1)/(2)\right)(-x)+((1)/(2)\left((1)/(2)-1\right))/(2*1)(-x)^2+((1)/(2)\left((1)/(2)-1\right)\left((1)/(2)-2\right))/(3*2*1)(-x)^3\\\\&= 1-(1)/(2)x+(-(1)/(4))/(2)(x^2)+((3)/(8))/(6)(-x^3)\\\\&= 1-(1)/(2)x-(1)/(8)x^2-(1)/(16)}x^3\\\\\end{aligned}`

`\textsf{To evaluate $\left((100)/(98)\right)^{(1)/(2)}$, compare $\left((100)/(98)\right)^{(1)/(2)}$ with $(1-x)^{(1)/(2)}$:}`

`\begin{aligned}\left((100)/(98)\right)^{(1)/(2)}&=(1-x)^{(1)/(2)}\\\\(100)/(98)&=1-x\\\\(98+2)/(98)&=1-x\\\\(98)/(98)+(2)/(98)&=1-x\\\\1+(1)/(49)&=1-x\\\\(1)/(49)&=-x\\\\x&=-(1)/(49)\end{aligned}`

`\textsf{Substitute $x = -(1)/(49)$ into the expansion of $(1-x)^{(1)/(2)}$ to evaluate $\left((100)/(98)\right)^{(1)/(2)}$:}`

`\begin{aligned}\left((100)/(98)\right)^{(1)/(2)}&= 1-(1)/(2)\left(-(1)/(49)\right)-(1)/(8)\left(-(1)/(49)\right)^2-(1)/(16)\left(-(1)/(49)\right)^3\\\\&= 1+(1)/(98)-(1)/(8)\left((1)/(2401)\right)-(1)/(16)\left(-(1)/(117649)\right)\\\\&= 1+(1)/(98)-(1)/(19208)+(1)/(1882384)\\\\&=1.01015255...\\\\&=1.010\; \sf (3\;d.p.)\end{aligned}`

`\textsf{Therefore, the evaluation of $\left((100)/(98)\right)^{(1)/(2)}$ to three decimal places is:}`

`\large\boxed{\boxed{1.010\;\sf(3\;d.p.)}}`