Question

Find the radius (r) of an aluminum cylinder that is 2.60 cm long and has a mass of 11.0 g. For a cylinder, V=πr²l. (The density of aluminum is 2.70 g/cm³.) Express the radius to three significant figures and include the appropriate units.

Answer 1

0.706 cm

Step-by-step explanation:

The question asks for the radius 'r' of an aluminum cylinder that is 2.60 cm long and has a mass of 11.0 g, given the formula for the volume of a cylinder and the density of aluminum as 2.70 g/cm³. To solve for the radius, we'll first find the volume of the cylinder using its mass and density, and then we'll use that volume to find the radius using the formula for the volume of a cylinder.

`\hrulefill`

Find the Volume of the Cylinder
`\hrulefill`

The volume 'V' of a substance can be determined using its mass 'm' and density 'ρ' through the formula:

`\rightarrow V = (m)/(\rho)`

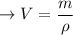
For the aluminum cylinder, m = 11.0 g and ρ = 2.70 g/cm³.


`\Longrightarrow V = (11.0 \ g)/(2.70 \ g/cm^3)\\\\\\\\\therefore V = 4.07407 \ cm^3`

`\hrulefill`

Find the Radius using Volume
`\hrulefill`

We're given the formula for the volume of a cylinder:

`\rightarrow V = \pi r^2 l`

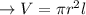
Isolating 'r', we get:

`\rightarrow r=\sqrt{(V)/(\pi l ) }`

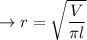
Given V = 4.0741 cm³ and l = 2.60cm, we can now find 'r':

`\Longrightarrow r=\sqrt{(4.0741 \ cm^3)/(\pi (2.60 \ cm) ) }\\\\\\\\\Longrightarrow r = 0.706241\\\\\\\\\therefore \boxed{r \approx 0.706 \ cm} \ \text{(3 s.f)}`

So, the radius of the aluminum cylinder is 0.706 cm, expressed to three significant figures.