Question

Write the expression as either the sine, cosine, or tangent of a single angle. cos(pi/5) cos(pi/7)+sin(pi/5)sin (pi/7)​

Answer 1

cos(2π/35)

General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Pre-Calculus

• Sum/Difference Formula [cosine]:
  `\displaystyle cos(x \pm y) = cos(x)cos(y) \mp sin(x)sin(y)`

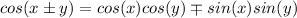
Explanation:

Step 1: Define

Identify

cos(π/5)cos(π/7) + sin(π/5)sin(π/7)

Step 2: Simplify

1. Sum/Difference Formula [cosine]: cos(π/5)cos(π/7) + sin(π/5)sin(π/7) = cos(π/5 - π/7)
2. Subtract: cos(π/5 - π/7) = cos(2π/35)