Answer:
12.85 ft
Explanation:
The total area of the window is the sum of the area of a semicircle with a diameter of x feet, and the area of a square with side lengths of x feet.
The formula for the area of a semicircle with radius r is:

The formula for the area of a square with side length x is:

As the diameter of the semicircle is equal to the side length of the square, and the diameter of a circle is twice its radius, the radius of the semicircle is x/2 feet.
Therefore, the equation for the area of the window is:
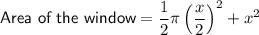
Given that the total area of the window is 230 ft², we can substitute 230 into the equation and solve for x:
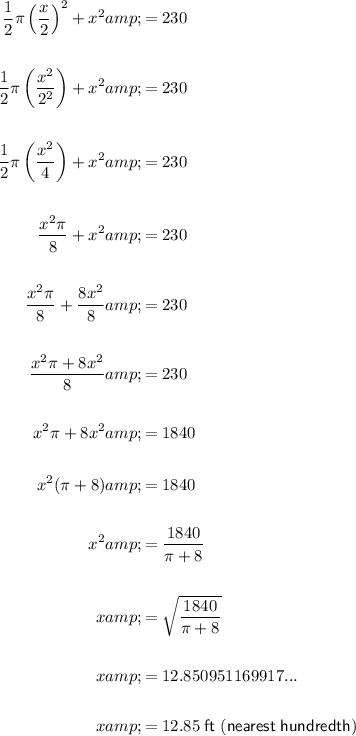
As x is equal to the width of the window, the width of the window is 12.85 ft (rounded to the nearest hundredth).