Question

Identify the function as a power function, a polynomial function, or neither. f(x) = 2 x (x + 2) (2 – 1)2 A power function O A polynomial function that is not a power function Neither a power function nor a polynomial function Show your work and explain how you arrived at your answer. Equation Editor EEEE A-AT, BIUS X, ** Styles Font Size Words: 0

Answer 1

The function f(x) = 2x(x + 2)(2 - 1)^2 is a polynomial function that is not a power function.

Step-by-step explanation:

The function f(x) = 2x(x + 2)(2 - 1)^2 is a polynomial function that is not a power function.

A power function is a function in the form f(x) = ax^n, where a and n are constants. In this case, the function does not have a constant and a variable raised to a power, so it is not a power function.

A polynomial function is a function that can be written as a sum of terms, each term consisting of a constant multiplied by a variable raised to a non-negative integer power. The given function can be expanded and written as a polynomial function, so it is a polynomial function.

Answer 2

The function f(x) = 2x ( x + 2) (x - 1)² is a polynomial function that is not a power function.

Identification of functions.

A function f(x) is said to be defined if each set of input variables (domain) is assigned to a specific output variable (co-domain).

In the given function:

f(x) = 2x ( x + 2) (x - 1)²; we are to identify if the function is a power function, a polynomial function, or neither.

To do that, we need to solve the function by using the following steps.

f(x) = 2x ( x + 2) (x - 1)²

f(x) = (2x² + 4x ) (x² - 2x + 1)

f(x) = 2x⁴ - 4x³ + 2x² + 4x³ - 8x² + 4x

f(x) = 2x⁴ - 6x² + 4x

A power function takes the form
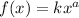`f(x) = kx^a`, thus we can't agree that the above function as a power function.

Similarly, a polynomial function can be expressed using the general formula:

`f(x) =a_0x^n + a_1x^(n-1) + a_2 x^(n-2) + ...+ x+1`

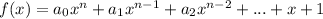
Therefore, we can conclude that the function:

f(x) = 2x ( x + 2) (x - 1)² = 2x⁴ - 6x² + 4x is a polynomial function that is not a power function.