Answer:
d) 165°

Explanation:
The interior angle of a regular polygon can be calculated using the following formula:

Therefore, to find the interior angle of a regular octagon, substitute n = 8 into the formula:
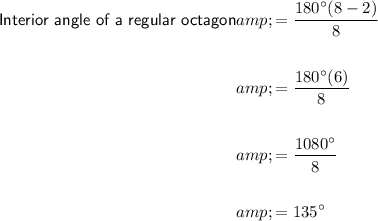
Therefore, the interior angle of a regular octagon is 135°.
The sides of the triangle in the given diagram are congruent (indicated by the tick marks). Therefore, the triangle is an equilateral triangle. Each interior angle of an equilateral triangle is 60°.
To find the measure of ∠JKL, we can subtract the measure of the interior angles of a regular octagon and an equilateral triangle from 360°.
Therefore:
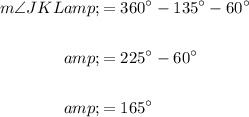
Therefore, the measure of ∠JKL is 165°.