Final Answer:
The volume of the solid bounded by the region in the xy-plane, the parabola
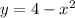 , the line
, the line
 , and the plane
, and the plane
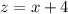 is
is
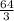 cubic units.
cubic units.
Step-by-step explanation:
To find the volume of the solid, first determine the limits of integration by finding the points of intersection between the parabola and the line. Set
 to find the intersection points:
to find the intersection points:
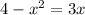
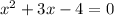
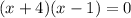
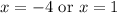
The limits of integration for x are from -4 to 1. Now, set up the integral to find the volume using the formula for volume of a solid of revolution:
![\[V = \int_(-4)^(1) A(x) \, dx\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/2nr44maeyx6nwd95ogasaci3zgvr6pw2b4.png)
The area of the cross-section at a given x-value is the difference between the functions:
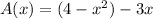 . Thus, the integral becomes:
. Thus, the integral becomes:
![\[V = \int_(-4)^(1) ((4 - x^2) - 3x) \, dx\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/u0249hfmky2y7g0wdl7qeo8x1kx12x1aoh.png)
Solve the integral:
![\[V = \int_(-4)^(1) (4 - x^2 - 3x) \, dx\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/nrji97bw3tgpv86qnalt8i5mgpybp1l6m0.png)
![\[V = \left[4x - (x^3)/(3) - (3x^2)/(2)\right]_(-4)^(1)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/wfu5rl30aw0rnvd9obpokykyoe829f13cw.png)
![\[V = \left[(4 - (1)/(3) - (3)/(2)) - (-16 + (64)/(3) + 24)\right]\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/9afgdufo2j31rf35sy6jl07t2rxnzr7o9d.png)
![\[V = (64)/(3)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/wkuji75tad6qk6bmt2dp0nywlep36cbt4q.png)
Therefore, the volume of the solid is
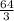 cubic units.
cubic units.