Question

A curve is described by the following parametric equations:

x= 4-t
y=t^2 -2

Answer 1

Option 3

Explanation:

Rearranging the first equations in terms of t, we get

t = 4 - x

Subbing this into eq 2,

y = (4 - x)² - 2

We can see from this that our curve is a quadratic in completed square form so it is a parabola with a vertex at the coordinates (4, -2).

Because the coefficient of x² is positive when expanding out this equation, it will have a U shape so traced from left to right for increasing values of t.

Answer 2

D) The curve is a parabola with a vertex at (4, -2) and is traced from right to left for increasing values of t.

Explanation:

A curve is described by the parametric equations:

`x= 4-t`

`y=t^2 -2`

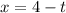
Rewrite the first equation to isolate t:

`t=4-x`

Substitute the expression for t (in terms of x) into the second equation to create an equation for y in terms of x:

`y=(4-x)^2-2`

`y=(-x+4)^2-2`

`y=(-(x-4))^2-2`

`y=(x-4)^2-2`

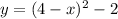
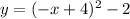
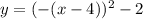
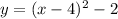
The vertex form of a parabola is y = a(x - h)² + k, where (h, k) is the vertex. Therefore, the equation for y in terms of x is in vertex form.

Comparing the equations, we can deduce that the vertex of the parabola is (4, -2).

To determine the direction the parametric parabola is traced for increasing values of t, we need to analyze the sign of the derivative of the x-coordinate (dx/dt) with respect to t.

Calculate the derivative of the x-coordinate with respect to t:

`x= 4-t \implies(dx)/(dt)=-1`

As dx/dt < 0, the x-coordinate is decreasing, and the curve traces from right to left as t increases.