Question

!50 POINTS! (3 SIMPLE GEOMETRY QUESTIONS)

QUESTIONS BELOW
|
|
\/

Answer 1

Question 1: C. 15 inches

Question 2: B. 342 meters

Question 3: D. 28.3 ft

Explanation:

Question 1:

We are given a triangle along with two side lengths (12 in and 9 in), which represent the short legs of the triangle, indicating that we are solving for the hypotenuse.

To find the hypotenuse of a right triangle we can use the pythagorean theorem which states that: a^2 + b^2 = c^2

In our case, it would be 9^2 + 12^2 = c^2

81 + 144 = c^2

225 = c^2

sqrt 225 = c

c = 15

So, x would be 15 inches.

Question 2:

Given a triangle with the hypotenuse of 1000m and an angle of 20 degrees for angle Q, we are solving for the length of RS. To do this, we can use sin since we need the opposite length as we are already given the hypotenuse length.

It becomes:

sin = opp/hyp.

sin 20 = x/1000

1000 sin 20 = x

x = 342.02

round to nearest meter

x = 342 meters

Question 3:

We are given a triangle with both short legs (15 ft and 24 ft), and solving for the length of the walkway which serves as the hypotenuse. Pythagorean theorem can be used here as well.

15^2 + 24^2 = c^2

225 + 576 = c^2

801 = c^2

sqrt 801 = c

c = 28.3

so the length of the walkway would be 28.3 ft

Answer 2

• 1st question: c. 15 inches.
• 2nd question: b. 342 m
• 3rd question: d. 28.3 ft

Explanation:

For 1st Question:

Since the diagonal of the kite bisect the diagonal perpendicular, which makes the right-angled triangle.

If it is right angled triangle we can use Pythagoras theorem.

Here,

Hypotenuse (h) = x

base(b) = 9 in

Perpendicular (p) = 12 in

we have

`\boxed{\sf h^2 = p^2+b^2}`

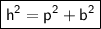
Now, substituting value

`\sf x^2 = 9^2+12^2`

`\sf x^2 =225`

`\sf x=√(225)`

`\sf x= 15`

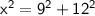
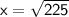
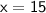
Therefore, answer is c. 15 inches.

`\hrulefill`

For 2nd question:

Given:

m ∡ Q =20°

m ∡ S =90°

`\sf \overline{\textsf{QR}} = 1000 m`

To find:

`\overline{\textsf{RS}} = \:?`

We can

In ΔQRS with respect to ∡Q

Hypotenuse (h) = 1000 m

base(b) =
`\overline{\textsf{QS}}`

Perpendicular (p) =
`\overline{\textsf{RS}}`

Since Relation between opposite or perpendicular and hypotenuse by sine angle rule.

We have,

`\sf Sin \:\angle Q = (Perpendicular)/(Hypotenuse)`

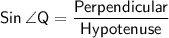
Substituting value

`\sf Sin 20^\circ = \frac{\overline{RS}}{1000}`

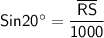
Doing Criss cross multiplications

`\sf \overline{\textsf{RS}} = Sin 20^\circ * 1000`

`\sf \overline{\textsf{RS}} \approx 342.02\: or \: 342`

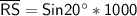
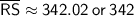
Therefore, answer is b. 342 m

`\hrulefill`

For 3rd question:

Since Opposite side are equal and all the angles are 90°.

here hypotenuse is walkway.

here,

Hypotenuse (h) =Walkway

base(b) = 24 ft

Perpendicular (p) = 15

We can use Pythagoras rule

we have

`\boxed{\sf h^2 = p^2+b^2}`

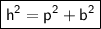
Now, substituting value

`\sf x^2 = 24^2+15^2`

`\sf x^2 = 801`

`\sf x =√(801)`

`\sf x \approx 28.3`

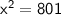
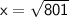
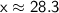
Therefore, answer is d. 28.3 ft