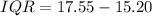Question

The hourly earnings (in dollars) for a sample of 25 railroad equipment manufacturers are:15.60 18.7514.60 15.8014.3513.90 17.5017.5513.8014.20 19.05 15.35 15.20 19.45 15.95 16.50 16.30 15.2515.05 19.10 15.20 16.22 17.75 18.40 15.25Find the median and the mode(s)(if they exist) of the data. What is the interquartile range

Answer 1

`Median = 15.80`

`Mode = 15.20\ \&\ 15.25`

`IQR = 2.35`

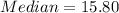
Explanation:

Given

`15.60,\ 18.75,\ 14.60,\ 15.80,\ 14.35,`

`13.90,\ 17.50,\ 17.55,\ 13.80,\ 14.20,`

`19.05,\ 15.35,\ 15.20,\ 19.45,\ 15.95,`

`16.50,\ 16.30,\ 15.25,\ 15.05,\ 19.10,`

`15.20,\ 16.22,\ 17.75,\ 18.40,\ 15.25.`

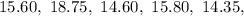
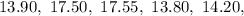
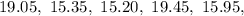
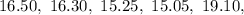
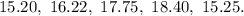
Solving (a): The median and the mode

First, we sort the data.

`13.80,\ 13.90,\ 14.20,\ 14.35,\ 14.60,\ 15.05,\ 15.20,\ 15.20,\ 15.25,\ 15.25,`

`15.35,\ 15.60,\ 15.80,\ 15.95,\ 16.22,\ 16.30,\ 16.50,\ 17.50,\ 17.55,\ 17.75,`

`18.40,\ 18.75,\ 19.05,\ 19.10,\ 19.45.`

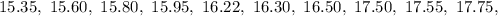
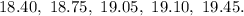
The median position is:

`Median = (n + 1)/(2)th`

`Median = (25 + 1)/(2)`

`Median = (26)/(2)`

`Median = 13th`

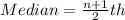
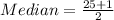
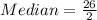
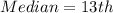
The 13th item is: 15.80

Hence:

`Median = 15.80`

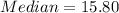
The modes are:

`Mode = 15.20\ \&\ 15.25` --- they both have frequency of 2 while others occur once

Solving (b): The interquartile range

This is calculated as:

`IQR = Q_3 - Q_1`

Since the median is at the 13th position, Q1 is:

`Q_1 = (1 + 13)/(2)th`

`Q_1 = (14)/(2)th`

`Q_1 = 7th`

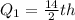
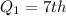
The 7th item is: 15.20

`Q_1 = 15.20`

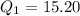
Similarly, Q3 is:

`Q_3 = (13+n)/(2)`

`Q_3 = (13+25)/(2)`

`Q_3 = (38)/(2)`

`Q_3 = 19th`

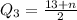
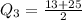
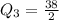
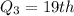
The 7th item is: 17.55

So:

`Q_3 = 17.55`

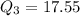
Hence,

`IQR = 17.55 - 15.20`

`IQR = 2.35`