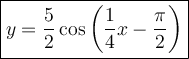Question

HELP W TRIG on the topic of phase shifts, amplitude, and period.

Answer 1

`y=(5)/(2) \sin \left((1)/(4)x\right)`

`y=(5)/(2) \cos \left((1)/(4)x-(\pi)/(2)\right)`

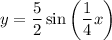
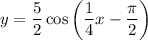
Explanation:

For the given equations of the form y = a sin(bx) or y = a cos(bx):

• "a" is the amplitude. It is the vertical distance from the midline of the curve to the peak (or trough).
• "b" is the frequency. It is the number of cycles the function completes in a given interval (usually 2π).
• 2π/b is the period. It is the horizontal length of one cycle of the curve.

The midline of a sinusoidal function is a horizontal line that is located exactly midway between the minimum and maximum y-values of the function.

From inspection of the graphed function, the maximum y-value is 5/2, and the minimum y-value is -5/2. Therefore, the midline of the graphed function is y = 0. This means that the amplitude is a = 5/2.

Graphically, the cosine function and the sine function have the same shape but the cosine function is the sine function shifted π/2 units horizontally to the left (a "phase shift" of π/2).

The midline of the parent sine function is y = 0, and y = sin(x) passes through the origin, whereas the parent cosine function passes through (0, 1), which is its maximum. Therefore, since the graphed function passes through the origin without a phase shift, the simplest equation to use for the graphed function is y = a sin(bx).

The period of the graphed function is 8π. Therefore, the number of cycles the function completes in 2π is 1/4. So b = 1/4.

Therefore, an equation in the form y = a sin(bx) to describe the graphed function is:

`\large\boxed{y=(5)/(2) \sin \left((1)/(4)x\right)}`

`\hrulefill`

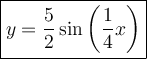
Additional information

To translate the parent cosine function so that its curve has the same orientation as the parent sine function, we need to shift the cosine function π/2 units to the right. Therefore, we subtract π/2 from the argument of the cosine function:

`\sin(x) = \cos\left(x - (\pi)/(2)\right)`

The period of the parent sine and cosine functions is 2π.

The period of the graphed function is 8π, which is 4 times the period of the parent function. Therefore, we need to subtract 4 times π/2 from the argument of the cosine function:

`y=(5)/(2) \cos \left((1)/(4)(x-2\pi)\right)`

`y=(5)/(2) \cos \left((1)/(4)x-(\pi)/(2)\right)`

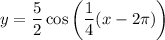
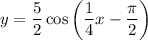
Therefore, an equation in the form y = a cos(bx) to describe the graphed function is:

`\large\boxed{y=(5)/(2) \cos \left((1)/(4)x-(\pi)/(2)\right)}`