Question

A flexible vessel contains 65.8 L of gas at a pressure of 2.07 atm. Under the conditions of constant temperature and constant number of moles of gas, what is the pressure of the gas (in atm) when the volume of the vessel increased by a factor of 16.00

Answer 1

Answer: Pressure of the gas is 0.129375 atm when the volume of the vessel increased by a factor of 16.00.

Step-by-step explanation:

The formula for ideal gas equation is as follows.

`PV = Nk_(b)T`

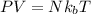
where,

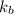`k_(b)` = Boltzmann constant

N = number of moles

That can also be written as:

`(PV)/(T) = constant`

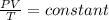
As pressure and volume are inversely proportional to each other. So, if one of the state variable is increased then the other one will decrease or vice-versa.

So, if volume of the vessel increased by a factor of 16.00 then it means pressure is decreased by a factor of 16.00

Therefore, final volume is as follows.

`65.8 L * 16.00\\= 1052.8 L`

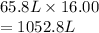
Now, final pressure is as follows.

`(2.07)/(16.00)\\= 0.129375 atm`

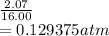
Initially the product of pressure and volume is as follows.

`PV = 2.07 * 65.8\\= 136.206`

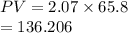
Hence, if volume of the vessel increased by a factor of 16.00 and pressure is decreased by a factor of 16.00 then its product is as follows.

`PV = 0.129375 * 1052.8\\= 136.206`

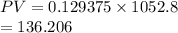
Here, product of pressure and volume remains the same.

Thus, we can conclude that pressure of the gas is 0.129375 atm when the volume of the vessel increased by a factor of 16.00.