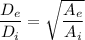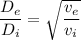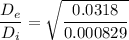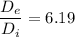Question

R-134a is throttled in a line flowing at 25oC, 750 kPa with negligible kinetic energy to a pressure of 165 kPa. Find the exit temperature and the ratio of the exit pipe diameter to that of the inlet pipe (Dex/Din) so that the velocity stays constant.

Answer 1

For R-134a, we are given :

`$T_i = 25^\circ C$`

`$P_i=750 \ kPa$`

`$P_e=165 \ kPa$`

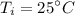
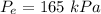
Now we have one inlet and one exit flow, no work and no heat transfer. The energy equation is :

`$h_e+(1)/(2).v_e^2= h_i+(1)/(2).v_i^2 $`

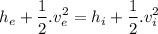
We also know that the gas is throttled and there is no change in the kinetic energy.

So,
`$v_e=v_i$`

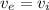
Now from the energy equation above, we can see that the inlet and the exit enthalpies are also the same. Therefore,

`$h_i=h_e$`

From the saturated R-134a table, corresponding to
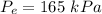`P_e = 165 \ kPa`, we can find the exit saturation temperature.

`$T_e=-15^\circ C$`

From the saturated R-134a table, corresponding to
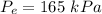`P_e = 165 \ kPa`, we can find the specific enthalpies :

`$h_f = 180.19 \ kJ/kg$`

`$h_(fg) = 209 \ kJ/kg$`

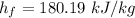
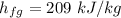
Calculating the exit flow quality factor,

`$x_e=(h_e-h_f)/(h_(fg))$`

`$=(234.59-180.19)/(209)$`

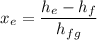
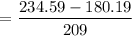
= 0.26

From the saturated R-134a table, corresponding to
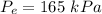`P_e = 165 \ kPa`, we can find the specific volumes :

`$v_f = 0.00746 \ m^3/kg$`

`$v_(fg) = 0.11932 \ m^3/kg$`

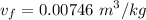
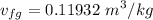
Calculating the exit specific volume :

`$v_e=v_f+x_e(v_(fg))$`

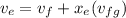
= 0.000746 + 0.26 (0.11932)

= 0.0318
`m^3/kg`

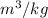
The mass flow is equal to :

`$\dot{m} = A_i . (v)/(v_i)$`

`$=A_e . (v)/(v_e)$`

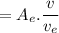
So,
`$(A_e)/(A_i)=(v_e)/(v_i)$`

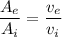
Therefore, the ratio of the exit pipe and the inlet pipe diameter is equal to

`$(D_e)/(D_i)=\sqrt{(A_e)/(A_i)}$`

`$(D_e)/(D_i)=\sqrt{(v_e)/(v_i)}$`

`$(D_e)/(D_i)=\sqrt{(0.0318)/(0.000829)}$`

`$(D_e)/(D_i)=6.19$`